Small World Netzwerke

0. Sechs Schritte

Die Ergebnisse eines in den späten 1960er Jahren von Stanley Milgram (1967) durchgeführten Briefexperiments popularisierten sich in der Phrase von den „Sechs Schritten“. Die hinter seinem Versuch stehende Frage war die nach der Nähe oder Entfernung sozialer Akteure im realen Leben. Wie viele Schritte muss eine Information auf direktem Weg transportiert werden, um von einem beliebigen Individuum zu einem anderen zu gelangen?

Das relativ einfach Setting des Versuches – zufällig ausgewählte Personen sollten einen Brief an eine andere Person weiterleiten, indem sie diesen an Bekannte [1] weiterleiteten – ergab, trotz der geringen Erfolgsquote von nicht einmal 20%, [2] ein erstaunliches Ergebnis: durchschnittlich hatte ein Brief, solange er dabei auf dem Gebiet der USA verblieb, die besagten sechs Schritte hinter sich, ehe er sein Ziel erreichte. Dabei spielten soziale Differenzen oder Entfernungen keine Rolle.

Ein ähnliches, wenn auch wesentlich differenzierter erfasstes Ergebnis lieferte die Wiederholung des Experiments mit Hilfe von Emails, das 2003 veröffentlicht wurde (Dodds/Muhamad/Watts, 2003). Hierbei wurden über 60.000 Nachrichten an 18 Zielpersonen in 13 unterschiedlichen Ländern versandt. Der Durchschnittswert lag wieder bei rund sechs Schritten.

Dieses Ergebnis überrascht angesichts der potentiellen Wegstrecken, durch die eine Information zwischen zwei Personen geleitet werden könnte. Der favorisierte Ansatz zur Erklärung dieses Resultats ist die Annahme so genannter Small World [SW] Netzwerke. Diese wurden in den letzten Jahren von unterschiedlichsten Wissenschaftsdisziplinen zur Erklärung verschiedener Phänomene benutzt. Neben den Sozialwissenschaften erschienen gerade auf dem Gebiet der Physik, aber auch der Mathematik und der Informationswissenschaft zahllose solcher Arbeiten.

Es soll im Folgenden ein kurzer Überblick zu diesem Phänomen gegeben werden. Im ersten Teil werden die Grundlagen zur Darstellung von SW-Netzwerken referiert und ihre Differenzen zu anderen Netzwerken herausgearbeitet. Im zweiten Teil sollen aktuelle Forschungen zu SW-Phänomen in Bezug auf das Internet, die Informationswissenschaft und spezieller auf die Webometrie vorgestellt werden. Die Probleme und Möglichkeiten, die sich mit SW-Netzwerken ergeben sind Thema des letzten Abschnittes.

1. Darstellung von Small World Netzwerken

1.1 Hubs and Vectors

Abbildung 1 Einfachste Darstellung der Ergebnisse von Milgram (1967) im Netzwerkmodell

Abbildung 2 Einfaches Netzwerk mit 9 Hubs (n=9)

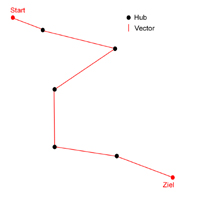
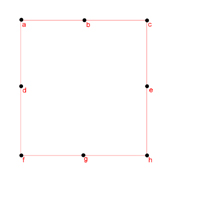
Um Netzwerke graphisch und mathematisch darstellen zu können, werden Hubs (Knoten) und Vectors (Vektoren) benötigt. Hubs sind dabei die Punkte, welche das Netzwerk bilden und Vectors die Verbindung zwischen zwei Hubs. [3] Im Beispiel des Milgramschen Briefexperiments würden demnach die einzelnen Menschen als Hubs und die Wege, welchen die Briefe genommen haben als Vectors dargestellt.

Abbildung 1 gibt dieses Ergebnis in der einfachsten möglichen Form wieder. Auffällig ist, dass hier, der Übersichtlichkeit halber, Start und Ziel angegeben sind, obwohl sich dies aus den Vektoren nicht schließen lässt.

Durch die Verbindungen zwischen den je benachbarten Punkten ergibt sich eine Verbindung aller sieben Hubs. Auf Grundlage dieser einfachen Darstellung können sich in einigen Schritten Modellen der SW-Netzwerke angenähert werden.

1.2 Einfache Netzwerke

Einfache Netzwerke zeichnen sich durch eine vollständige Egalität der Hubs und der Vektoren aus. Jeder Hub hat in ihnen gleich viele Vektoren und alle Vektoren haben die gleichen Eigenschaften, das heißt zuerst einmal die gleiche Länge. Dies ist in Abbildung 2 dargestellt. Jeder Hub hat hier genau zwei Vektoren, die gleich lang, gleich stark und ungerichtet sind. Würde man in dieses Netzwerk mehr Hubs mit den gleichen Eigenschaften integrieren, würde sich nach und nach eine Kreisform ergeben, welche in den meisten Erläuterungen solcher Netzwerke abgebildet sind. [4]

Allerdings lässt sich mit diesem Modell noch reichlich wenig über die SW aussagen. In einem solchen einfachen Netzwerk wie im Beispiel würde die Strecke, die eine Nachricht zurücklegen müsste, um von einem Punkt zum anderen zu gelangen davon abhängen, wie viele Nachbarn zwischen den beiden Punkt liegen. Dieser Weg ist als Länge oder auch Distanz mit der Variable L angegeben. So ist der kürzeste Weg zwischen g und f genau L=1, da diese keinen Hub zwischen sich haben, während der kürzeste Weg von e nach f, zwischen denen h und g liegen, 3 Schritte (L=3) beinhaltet. Diese Zahl steigt expotential mit der Anzahl der Hubs. Der durchschnittliche Wert von 6, den Dodds, Muhamad & Watts (2003) und Milgram (1967) fanden, wäre, wenn die Gesellschaft in dieser Weise organisiert wäre, nicht zu erreichen.

1.3 Komplexe Netzwerke

1.3.1 Erdös-Renyi

Abbildung 3 Erdös/Renyi Zufallsgraph

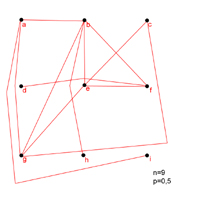
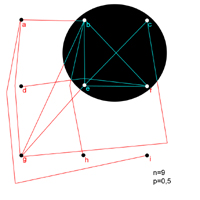
Komplexe Netzwerke entstehen durch die Modellierung von Eigenschaften der Vectors und der Hubs. Erdös-Rényi [5] Zufallsgraphen sind der erste Schritt in diese Richtung. Hier werden den Hubs die Vektoren mit der Wahrscheinlichkeit p zugeteilt. p=0,5, wie in Abbildung 3 verwendet, bedeutet, dass jede mögliche Verbindung zwischen den vorhandenen Hubs mit dem Wahrscheinlichkeitswert von 0,5 gesetzt wurde. Dies bedeutet unter anderem, dass die Hubs unterschiedlich viele Vectors haben können. In diesem Beispiel sind das bei e=4, c=2 und i=1.

Wir sehen in der graphischen Darstellung, dass sich langsam das Bild eines Netzes ergibt. Mit diesem Modell waren Erdös und Renyi in der Lage nachzuweisen, dass es nur einer relativ geringen Zahl an Vektoren bedarf um eine Ansammlung von Hubs so zu verbinden, dass sie ein vollständiges Netzwerk ergeben, indem jeder Hub von jedem anderen Hub aus, nur über die Vektoren, erreicht werden kann.

1.3.2 Cluster

Das Beispiel in Abbildung 3 zeigt uns zudem das Entstehen von Clusters, dass sind miteinander in höherem Maße, als im gesamten Netzwerk üblich, verbundene Hubs. Solche Klumpungen können erst durch die Aegalität der Knoten entstehen. So bilden im dargestellten Netzwerk die Punkte b, c, e und f ein Cluster, während die Punkte d,e,g und h keines darstellen.

Abbildung 4 Beispiel eines Clusters

Der Clustering Coefficient [CC] C ist dabei definiert als die Wahrscheinlichkeit, mit der ein Hub (a), der schon mit einem anderen Hub (b) verbunden ist, mit einem weiteren, dritten Hub (c) verbunden ist, welcher wiederum schon mit dem zweiten (b) einen gemeinsamen Vektor hat. Das ist im Beispiel zwischen b, e und f der Fall. Solche Triangles können als Wert für die Dichte von Netzwerken betrachtet werden. Für einen Hub wird C wie folgt berechnet: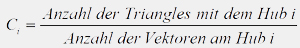

Insoweit kann C den Wert von 1 nie übersteigen. Der globale Clustering Coefficient eines gesamten Netzwerkes ergibt sich aus dem Zusammenziehen der CCs aller Hubs.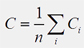

Dieser globale Wert C lässt sich selbstverständlich auch für Bereiche von Netzwerken berechnen, wobei Cluster einen signifikant höheren CC haben, als nicht oder nur schwach geclusterte Bereiche. [6] Dies bedeutet auch, dass in jedem Netzwerk neu zu bestimmen ist, welche Klumpung von Hubs ein Cluster ist und welche eventuell noch nicht.

1.3.3 Barabási-Albert

Eine fundamentale Erweiterung, welche aus Modellen komplexer Netzwerke Werkzeuge zur Beschreibung realer Netzwerke macht, lieferten Barabási und Albert (1999). In ihrem Modell wird die Ungleichheit der Hubs systematisch erhöht. Ob ein Hub mit einem anderen Hub einen gemeinsamen Vektor erhält ist nicht mehr zufällig geregelt. Je reicher ein Knoten schon ist, dass heißt, je mehr Vectors er schon hat, umso größer ist die Wahrscheinlichkeit, dass er weitere Vektoren erhält. Diese rich-are-getting-richer Regel führt, in zweidimensionale Diagramme übertragen auch sichtbar, zu den Potenzfunktionen folgenden Verteilungen.

Dieses Phänomen hatte Derek de Solla Price schon in den 1960er Jahren für die Zitationshäufigkeit von wissenschaftlichen Artikeln beschrieben. Allerdings sind, wie Newman (2003, pp.213f-215) bemerkt, seine Ergebnisse erst nach dem Erfolg des Modells von Barabási und Albert (wieder) entdeckt worden.

Solche Netzwerke, bei denen es keine regelmäßige Verteilung der Vectors mehr gibt, werden Scale-Free Networks oder skalenfreie Graphen genannt. Ihnen eigen ist eine relativ große Stabilität. Diese bedeutet, dass das zufällige Entfernen von Hubs eine viel geringere Auswirkung auf die Werte L und C hat, als in den anderen vorgestellten, nicht-skalenfreien Netzen mit dem gleichen Wert n. Dies ist durch die Existenz reicher Hubs zu erklären. Solange nicht genau sie ausfallen, nehmen sie für die Wege von Informationen, die durch L angegeben werden, eine Knotenfunktion ein, die es derart in einfachen Netzwerken nicht geben kann.

1.3.4 Weitere Modulationen

Den Modifikationen von Albert und Barabási folgten weitere, zumeist mit dem Ziel, mit den jeweiligen Modelle die Realität genauer abbilden zu können. Es wurden Modelle entworfen, in welche eine Maximalzahl der Vektoren pro Hub festlegt wurde, in anderen wurde die mögliche Distanz zwischen zwei Hubs, die direkt miteinander verbunden sind, begrenzt (Goh, Kahng, Kim, 2005).

Hervorzuheben ist die Angabe der Richtung von Vectors. In den bisher vorgestellten Modellen waren diese ungerichtet. In den darauf folgend entwickelten konnten sie nicht nur in eine oder beide Richtungen wirken, sondern durch diese Modifikationen weitere Differenzierungen zwischen den Hubs ermöglichen. So kann zum Beispiel ein Knoten mit mehr auf ihn verweisenden Vektoren eine höhere Wahrscheinlichkeit erhalten, neue Verbindungen zu erlangen, als ein Hub mit mehr ausgehenden, als eingehenden Vektoren.

Ebenso wird die Gewichtung von Vectors betrieben. Dass heißt, ein Vektor kann stärker oder schwächer und somit mehr oder minder bedeutsam sein.

Andere Ansätze statten die Hubs mit unterschiedlichen Eigenschaften aus, die sich auf die Wahrscheinlichkeit von neuen Vektoren auswirken. Die Statik der Modelle wurde, durch die Einführung von Variablen zur Flüchtigkeit von Verbindungen zwischen oder auch der Existenz von Hubs, versucht aufzuheben.

All diese Veränderungen wurden durch die Beobachtung realer Netzwerke notwendig. In den Experimenten mit den Modellen stellt sich durchgängig heraus, das sie zwar Ansätze liefern können, um das von Milgram aufgeworfene Problem zu lösen, aber immer weit von einer endgültigen Lösung entfernt sind.

1.4 Small World

Ravid and Rafaeli (2004) untersuchten asynchrone Diskussionsgruppen im Internet mit dem Ergebnis, dass diese Small World Netzwerke seien. Solche Netzwerke, so fassen die beide Autoren zusammen, haben eine geringe durchschnittliche Distanz (L) und einen höheren Clustering Coefficent (C) als simulierte Zufallsgraphen mit der gleichen Anzahl Knoten (n). [8] Diese Definition ist in der einen oder anderen Form allgemein akzeptiert. L lässt sich in diesen Netzwerken mit bestimmen (Adamic, Adar, 2005, p.189).

Ihre, in Tabelle 2 dargestellten und ähnlich immer wieder gefundenen, Ergebnisse warfen bedeutende Fragen auf. [9] Wie kann die Distanz so immens kleiner und gleichzeitig der CC so signifikant größer sein, als in künstlich erstellten Netzen? Wie sind solche Netzwerke zu simulieren? Und für Ravid und Rafaeli: Warum funktioniert diese Aussage gerade in ihrer Untersuchung nicht?

Abbildung 5 Small World Netzwerk mit n=9 und egalitären Vektoren

Abbildung 6 Ausschnitt der Daten der OPTE Datenbank (10%) vom 15.01.2005. Eine anderes Beispiel für eine Small World.

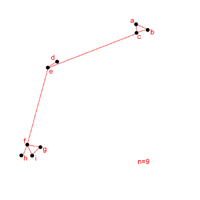
Die Antwort auf diese Fragen wurde durch Watts and Strogatz (1998) gegeben, war aber schon in den 1970er Jahren durch Mark Granovetter formuliert worden. Der Unterschied bei diesen beiden Antworten war, dass Granovetter als Soziologe an die Forschungen von Milgram anschloss und als solcher von der Mathematik und Physik nicht beachtete wurde, während Watts und Strogatz (1998) als mathematisch orientierte Soziologen schrieben –zudem publizierten sie in Nature, wo sie auch über die Soziologie hinaus wahrgenommen werden konnten. Ihre Arbeit wurden weithin beachtet [10] und lösten eine rege Forschungstätigkeit auf unterschiedlichen Gebieten aus.

Ihr Ansatz vereint die Zufallsgraphen mit den gerichteten, einfachen Netzwerken. Dies, so ihre These, würde dem Wachstum sozialer und anderer Netzwerke entsprechen. So würden sich immer wieder starke Cluster bilden, die allerdings über einzelne Hubs in diesen Clustern wieder untereinander verbunden sind. Genau dies hatte Granovetter mit den Begriffen Bridge und the Strength of Weak Ties beschrieben. [11]

Abbildung 5 zeigt ein solches Netzwerk, dass allerdings mit n=9 relativ klein ist und sich alle Vektoren egalitär verhalten. Abbildung 6 dagegen stellt ein komplexeres Small World Modell vor. [12] In ihrem Artikel führten Strogatz und Watts dies am Netzwerk der Schauspielerinnen und Schauspieler, die in der Internet Movie Database verzeichnet sind - wobei die einzelnen actors die Hubs darstellen, die einen Vektor erhalten, so sie zusammen in einem Film spielten [13] - und am Elektrizitätsnetzwerk im Westen der USA aus. Diese beiden Beispiele wurden in Texten zu Small World Networks populär.

2. Aktuelle Forschungen

2.1 Frühe Formen

Schon vor dem durch Watts und Strogatz ausgelösten Boom von wissenschaftlichen Artikeln über die Small World [14], gab es andere, relativ bekannte Anwendungen der Milgramschen Fragestellung.

2.1.1 Erdös Number

Abbildung 7 Weltweite Verteilung der Erdös Number

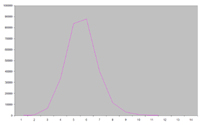
Die Erdös Number ist eine Darstellung des weltweiten Netzwerkes von Mathematikerinnen und Mathematikern. Ausgehend von Pál Erdös, welcher die Erdös-Rényi-Netzwerke mit entworfen hatte, erhalten die Autorinnen und Autoren von mathematischen Artikeln eine Nummer. Dabei hat Erdös die Nummer 0, alle die mit ihm einen Artikel geschrieben haben (wie zum Beispiel Alfréd Rényi) die Nummer 1. Diejenigen, die wiederum mit Personen mit der Erdös Number 1 einen Artikel veröffentlichten, erhalten die Nummer 2 und so weiter. Die durchschnittliche Erdösnummer ist, bei 268015 Menschen, die überhaupt eine besitzen, ≈5, genauer 4,65. [15] In Abbildung 7 ist die Verteilung dieser Nummer graphisch dargestellt. Die Häufung ist deutlicht zu erkennen. Dies sind zwar nicht die sechs Schritte, welche Milgram aus seinem Experiment berichtet hatte, dafür sind hier bedeutend weniger Menschen beteiligt, die zudem mindestens einen ähnlichen Bildungshintergrund haben und somit diese Barriere nicht überwinden müssen, wie es die Briefe von Milgram taten. Außerdem war Erdös mit fast 1.400 publizierten Artikeln und einer besonders nomadischen Lebensweise eine Ausnahmefigur, die so in anderen Netzwerken nicht gefunden werden kann. Seit Erdös 1996 starb ist es fernerhin nicht mehr möglich die Erdös Number 1 zu erlangen. Trotzdem zeigt dieses Beispiel, wie relativ klein die Welt, zumindest die der Mathematik, sein kann. Die Abbildung zeigt uns ein weiteres Merkmal der Small World Netzwerke: die Verteilung von Hubs und Vektoren folgt immer annähernd einzelnen Potenzfunktionen. Das ist bei Darstellungen von Daten aus SW-Netzwerken in Funktionsgraphen mit den Achsen Rank und Links pro Hubs ebenso. Dort bilden sich immer annähernd exponentielle Kurven.

2.1.2 Kevin Bacon Oracle

Eine andere bekannte Anwendung, die sich im Nachhinein mit Small World Theoremen erklären lässt, ist das Kevin Bacon Oracle. Kevin Bacon, der als Schauspieler in nun schon über 50 Filmen mitgespielt hat, sei, so die nicht ganz ernst zu nehmende Theorie, das Zentrum von Hollywood. Bewiesen wurde dies anhand eines kleinen Programms, welches der Student Brett C. Tjaden geschrieben hatte und das sich aus den Daten der auch von Watts und Strogatz verwendeten Internet Movie Database speist. Das System funktioniert ähnlich der Erdös Number. Wer immer mit Bacon in einem Film mitgespielt hat, erhält die Bacon Number 1, wer mit solchen Leuten in einem Film spielte die Number 2. Das Ergebnis, ist, getreu der Verschwörungstheorie, nach der Bacon Hollywood beherrscht, erschreckend, da die durchschnittliche Bacon-Number gerade einmal 2.953 beträgt. Eine graphische Darstellung wäre der Abbildung 7 ähnlich. [16]

Allerdings, und dies widerlegt die Theorie, hat man heute die Möglichkeit mit der Suchmaschine, die aus dem kleinen Programm entwickelt wurde, alle Schauspielerinnen und Schauspieler Hollywoods miteinander zu vergleichen und erhält ähnliche Ergebnisse. Das „Geheimnis“ hinter diesem Netzwerk ist ebenfalls, dass es sich um ein relativ kleines Small World Netzwerk handelt. [17]

2.2 Forschungsfragen

Neben solchen, eher amüsanten Anwendungen, gab und gibt es vor allem ernsthafte Überlegungen, Erkenntnisse aus den Theoremen über Netzwerke zu ziehen. Sie bieten die Möglichkeit komplexe Probleme zu klären.

2.2.1 Stabilität

Die relativ hohe Stabilität von realen Netzwerken bei gleichzeitig relativ geringer Distanz ihrer Knoten zueinander - das gilt für das Internet, sowohl als technisches Netzwerk von Netzwerken aus Computern, als Netzwerk von Links und als soziales Netzwerk, [18] als auch für Freundschaftsnetzwerke in Bildungseinrichtungen, [19] Nahrungsnetze, [20] den Flug- und Personennahverkehr [21] oder anderen - findet im Ansatz von Watts und Strogatz ein tragfähiges Modell. Wenn fast alle Verbindungen zwischen Hubs in zufällig zusammengesetzten Clustern organisiert sind und nur relativ wenige Vektoren die größeren Distanzen überwinden, werden die Netzwerke weniger anfällig, falls zufällig Vectors oder Hubs entfernt werden. Diese Stabilität zu verstehen kann viel helfen, sie absichtlich herbei zu führen, um oben genannte Netze in dieser Stabilität zu halten. Pinheiro und Bernades (2005) wollen zum Beispiel diese Eigenschaften für die industriellen Herstellung von Materialien nutzbar machen.

Gleichzeitig hat diese Stabilität einen Schwachpunkt gegenüber den einfachen und den komplexen Netzwerken: Wenn die schwachen Vectors oder reichen Hubs mit großer Distanz gezielt entfernt werden, bricht die Stabilität des jeweiligen Small World Netzes schneller und gravierender zusammen, als andere Netze bei gleichen Maßnahmen. [22] Dies zu verstehen ist zum einen notwendig, um solche Ausfälle, zum Beispiel einen scheinbar unwichtigen, aber durch seine Vektoren mit großer Distanz doch wichtigen Server in einem LAN-Netzwerk oder aber einer für das Ökosystem einer Region immanent wichtigen Pflanzenart, zu erkennen und zu beheben.

Gleichzeitig lassen sich ähnliche Netzwerke bei der Verbreitung von Krankheiten feststellen. Hier kann es für die Biologie, Zoologie, Medizin oder Ökologie genau darum gehen, solche aus den Clustern herausführenden Hubs zu lokalisieren und zu isolieren, um die Epidemie wirksam und sicherer als bisher einzudämmen (Christley et. al. (2005).

Qin et. al. (2005) versuchen mit der Netzwerktheorie gar terroristische Gruppen zu analysieren und damit ein Mittel zu schaffen, solche Gruppe mit relativ wenig Aufwand zu schwächen.

2.2.2 Navigation in Small World Netzwerken

Wenn wir ein SW-Network als Graphen darstellen, können wir versuchen, die jeweils kürzeste Distanz zwischen zwei Hubs zu finden. Wir sind, mit einigen mathematischen Kenntnissen, in der Lage schon vor unserer Suche zu sagen, wie groß die Distanz höchstwahrscheinlich sein wird. Allerdings, und das ist ein akutes Forschungsproblem, konnten das die Menschen, die an Milgrams und später an Dodds’, Muhamads & Watts’ Experiment teilnahmen nicht. Sie hatten einzig „lokales Wissen“ von ihren persönlichen Netzwerken und schafften es dennoch eine Distanz von L≈6 zu finden. Es stellt sich die Frage, wie nur anhand lokalen Wissens in Small World Netzwerken navigiert werden kann, so wie es soziale Akteure offensichtlich können. [23]

Bisher scheint diese Frage noch ungelöst. Adamic und Adar (2005) untersuchten in einem Experiment drei Thesen, welche in den letzten Jahren zu dieser Frage aufgestellt wurden:

1. Menschen verteilen Nachrichten effektiv, indem sie sie an Menschen weitergeben, die viele Kontakte haben (und damit rich hubs darstellen).
2. Menschen können Nachrichten effektiv verteilen, wenn sie ihnen bekannte Hierarchien bei der Verteilung nachvollziehen, dass heißt die Nachrichten an Menschen geben, die aufgrund ihrer Stellung höchstwahrscheinlich mehr Kontakte haben.
3. Menschen können Nachrichten effektiv verteilen, wenn sie sich geographisch orientieren, das heißt, die Nachricht Menschen geben, welche sich höchstwahrscheinlich näher am Zielpunkt der Information befinden.

Das Ergebnis war negativ. In einem relativ klein Netzwerk aus 430 Mitgliedern mit einer errechneten durchschnittlichen Distanz von L=3,1 ergaben alle drei Suchstrategien signifikant höhere Ergebnisse, wie Tabelle 3 zeigt.

Die beiden Autoren schließen daraus, dass offenbar andere Search Strategies verwendet wurden. Dabei heben sie vor allem die Annahme hervor, dass Individuen höchstwahrscheinlich, trotz der Beschränkung auf lokales Wissen, weiter als nur einen Schritt denken.

Doods, Muhamad & Watts bemerken in der Auswertung einer Studie, das nicht, wie bis dahin angenommen, die Existenz von „rich hubs“ für eine Navigation in sozialen Netzwerken nötig sei und das „Network structure alone is not everything“ (Doods/Muhamad/Watts, 2003, p. 829).

Das Verständnis solcher Vorgänge könnte zahlreiche positive Effekte zeitigen. Ist der Informationsfluss innerhalb und zwischen sozialen Gruppen bekannt, kann eine Verteilung von Information auf einem effektiveren Weg erfolgen, als es bisher geschieht. Das sollte nicht nur als Möglichkeit für die Werbeindustrie verstanden werden. Wu et.al. (2004, p.327) heben die möglichen ökonomischen Effekte in einer immer mehr auf Informationen aufbauenden Gesellschaft hervor. Es wäre denkbar auf diesen Erkenntnissen basierend Search Engines mit anderen Such- und Bewertungsstrategien als bisher zu programmieren. (Palotai/Farkas/Lõrincz, 2005) Andere Analysen versuchen, durch das Verstehen der sozialen Beziehungen als Small World oder ähnlichen Netzwerken für Informationseinrichtungen Zugangsmöglichkeiten für Bevölkerungsgruppen zu etablieren, die bisher aus unterschiedlichen Gründen von – für sie notwendigen – Informationen ausgeschlossen sind. [24]

2.2.3 Evolution

Ein bisher wenig bearbeitete Frage ist die nach der Evolution von komplexen Netzwerken (Zhu/Huang, 2004, p.036117-8). Zwar ist es möglich, im Nachhinein die Genealogie von Netzwerken nachzuvollziehen, doch scheint bisher nicht möglich ausreichend genau vorauszusagen, wie Netzwerke sich entwickeln werden. Ein Ansatz ist das Postulat, dass das rich-is-getting-richer Phänomen die Ausprägung von SW-Netzen bedingt (Buchanan, 2002, pp.109-112). Dabei könnte eine genauere Bestimmung dazu ermächtigen Cluster und Teile von Netzwerken gezielt zu Wachstum, Abnahme oder Transformation zu stimulieren.

Der Nutzen, welcher sich aus der Analyse von Netzwerken versprochen wird, könnte durch eine Kenntnis ihrer Evolution verstärkt werden. Gerade der Aufbau der Small World Netzwerke, teilweise strukturiert, teilweise zufällig, der sie so stabil und effektiv macht, macht allerdings solche Vorhersagen ungenau. [25]

2.2.4 Eingeschränkte Zufälligkeit

Die Applikation der Small World Theoreme auf Real World Netzwerke zeigt ein weiteres Problem auf: Die Zufälligkeit, nach der sich Cluster bilden ist keine einfache, sondern immer eine eingeschränkte.

Freundschaftsnetzwerke zeigen zum Beispiel bei genauerer Analyse das Wirken von auf sozialen Faktoren basierenden Ein- und Ausschlüssen. (Newman, 2003, pp. 190-195) Im Internet lassen sich ähnlich Strukturen finden, [26] aber auch bei der Untersuchung des Netzwerkes zwischen brasilianischen Fußballern (Onody/de Castro, 2004) oder dem Erfolg von musicians und physicists (Davies, 2002) wirken offenbar unterschiedliche Faktoren bei die Bildung von Clustern. Insoweit ist die Zufälligkeit von Verbindungen immer eine Zufälligkeit zwischen schon vorher prädestinierten „Hubs“.

Für die Netzwerktheorie ist das Problem dabei nicht die Existenz solcher Faktoren. Diese lassen sich als Variablen simulieren. Das Problem – wieder aus der Sicht der Netzwerktheorie - ist die Unstetigkeit und Veränderlichkeit dieser Variablen. Das oft herangezogene Beispiel von Netzwerken unter Schülerinnen und Schülern oder auch Studierenden in den USA offenbart dieses Problem: Viele dieser Netzwerke weisen eindeutig eine relativ hohe Segregation entlang der ethnischen Herkunft auf, andere eher die Segregation anhand des sozialen Status und wieder andere orientieren sich offenbar vor allem am Wohnort. Zum einen lässt sich bisher nicht vorhersagen, welche Faktoren in welchem Maße in jeder einzelnen Highschool oder Universität wirken, zum anderen steht zu erwarten, dass sich die Bedeutung dieser Faktoren mit der Zeit aus unterschiedlichen Gründen wandelt.

Solche unsicheren Faktoren, lassen sich in der Analyse nahezu aller Real World Netzwerke nachweisen, wobei sie oft nicht so offensichtlich sind, wie in den angeführten Freundschaftsnetzwerken. [27]

2.3 Internet und Zitationsanalysen

2.3.1 Internet

Das Internet, verstanden als Sammlung von Websites und anderen Onlinedokumenten, so wird mehrfach postuliert, ist eine Small World (Adamic/Adar, 2003). Dies ist bisher, aufgrund eines methodischen Problems bei der Gewinnung von Daten nicht bewiesen. Um ein Netzwerk als Small World charakterisieren zu können, müssen die Hubs untereinander verbunden sein. Im Internet geschieht die durch Links, die sich unterteilen lassen in:

• Inlinks, die auf eine Website oder ein Dokument verweisen.
• Outlinks, die von einer Website oder einem Dokument abgehen. In- und Outlinks sind in diesem Modell gerichtete Vektoren, während die Onlinedokumente Hubs darstellen.
• Und gelegentlich In- and Out-Links, das heißt Vektoren, zwischen zwei Seiten oder Dokumenten, die gegenseitig verlinkt sind.

Allerdings wurden bisher die Daten für die Analysen des Internets durch Suchmaschinen gewonnen, deren Robots neue Dokumente nur durch Links auf schon bekannten Seiten finden. Da Links immer gerichtet sind, [28] können auf diese Weise keine Dokumente, die nur Outlinks oder gar keine Links (Vektoren) besitzen, gefunden und somit auch nicht in die Analyse mit einbezogen werden. Demnach ist es nicht möglich eine Aussage über die Vollständigkeit der jeweils untersuchten Daten und somit über den SW-Status des Internets zu geben. [29]

Trotzdem sind das Internet, einzelne seiner Bereiche und mit ihm verbundene Dienste im WWW Gegenstand verschiedenster Forschungen, deren Ziel ist, entweder Produktion, Wachstum und Distribution von Informationen und Wissen nachzuvollziehen [30] oder aber das Internet als Abbild sozialer Netzwerke verstehen und versucht diese zu untersuchen [31]. Neben der Entwicklung von Suchstrategien [32] liegt der Schwerpunkt der Forschung in diesem Bereich auf dem Verständnis der Vorgänge im Netz selbst.

2.3.2 Bibliometrie / Webometrie

Ein weiteres Feld, in dem SW Netzwerke vermutet wurden, sind die in der Bibliometrie untersuchten Zitationsnetzwerke zwischen wissenschaftlichen Artikeln. In diesem Bereich konnten SW Netzwerke nachgewiesen werden, da zum Beispiel die Datenbanken wissenschaftlicher Artikel auch solche Dokumente verzeichnet, die nicht oder noch nicht zitiert wurden.

Allerdings ist die Verbindung zwischen Bibliometrie oder auch der Webometrie, die ähnliche scientometrische Verfahren auf Onlinedokumente anwendet und dem Mainstream der SW Forschung gering. Die von der Bibliometrie erarbeiteten Grundlagen wurden, wie schon beim Beispiel des rich-is-getting-richer Phänomens erwähnt, nahezu vollständig unbeachtet, oft ein zweites Mal formuliert und erst im Nachhinein in Überblicksartikeln referiert.

Trotzdem kann die Bibliometrie von den Forschungen zu SW-Netzwerken profitieren. Es sind mit diesen genauere Aussagen über Publikationen und ihre Verbindungen zu andern Dokumenten möglich.

3. Probleme und Möglichkeiten

Die Analyse des Small World Phänomens ist noch nicht abgeschlossen. Seit Watts and Strogatz (1998) ihren Lösungsansatz publizierten, hat es unzählige Forschungen auf diesem Gebiet gegeben. In einer weitgehend auf die Distribution von Informationen basierenden Gesellschaft kann dieses Wissen dazu beitragen, die Beziehungen innerhalb dieser besser zu verstehen. Ein Verständnis von Zusammenhängen in ökologischen Netzwerken ist unabkömmlich für ökologische Politik und umweltbewusstes Handeln. Die Dokumentation, vor allem der Zweig der Bibliometrie hat bisher dazu beigetragen, Redundanz von Informationen zu vermindern und wissenschaftliches Arbeiten effektiver zu gestalten. Die Forschungen an SW-Netzwerken können diese Effektivität weiter verbessern.

Allerdings wirft das Vorhandensein von Small World Netzwerken in der Gesellschaft auch Probleme auf. Wenn die Gesellschaft aus Individuen mit einer hohen Anzahl von Verbindungen, die dem Informationsfluss außerhalb ihrer Communities dienen, und Individuen ohne diese Verbindungen bestehen, ist zu fragen, ob hier eine gesellschaftlich nicht gewollte Ungleichmäßigkeit besteht. Eventuell widerspricht dies nicht nur dem Postulat der Chancengleichheit, sondern könnte zu einer nicht hinzunehmenden sozialen Schieflagen führen. Das ist gerade vor dem Hintergrund bedeutsam, das die Analysen von SW-Netzen die Bedeutung solcher Verbindung aufgezeigt haben.

Gerade auf dem Gebiet der Physik erschienen in den letzten Jahren Untersuchungen zu Small World Phänomenen aus den unterschiedlichsten Bereichen (Onody/de Castro, 2004). Es entsteht teilweise der Eindruck, als würde dieses Phänomen nicht nur als allgegenwärtig, sondern auch als alle Probleme lösender Ansatz verstanden (Buchanan, 2002). Dabei werden vor allem die Parallelitäten zwischen unterschiedlichen Netzwerken betont, auf die Differenzen dagegen wird kaum eingegangen. Wie viele andere Modelle, die einst als einheitliche Erklärung für unterschiedlichste Phänomene galten, scheint zurzeit die SW das Versprechen der allgemein Weltformel in sich zu tragen. Dem sollte, aus der Erfahrung, dass solche Weltformeln schließlich nie ihre impliziten Versprechen erfüllen konnten und dem Wissen, dass durch die umstandslose Anwendung solcher Konzepte oft bedeutsame Merkmale der Untersuchungsgegenstände übersehen werden, vorgebeugt werden. Das Partikulare würde sonst in der extremen Generalisierung verschwinden. Genau vor diesem Problem stehen Ravid und Rafaeli (2004), die ihre Ergebnisse nur zum Teil mit dem Theoremen zur SW erklären konnten, obwohl sie n den analysierten Discussion groups die SW-Architektur vorfanden. Die Reichweite der Erklärungen zur Small World sollten nicht überstrapaziert, sondern in ihrer Begrenztheit anerkannt und produktiv gemacht werden.

4. Schluss

Diese Arbeit gab einen Abriss über das Small World Phänomen. Im ersten Teil wurden, mit einer Steigerung hin zu komplexen Netzwerken, die Grundlagen der bedeutsamsten Netzwerk-Modelle referiert und die Besonderheiten der Small World Netzwerke herausgearbeitet. Daran anschließend wurden die wichtigsten Forschungsprobleme, die sich aus den Beobachtungen an solchen Netzwerken ergeben haben, dargestellt. Im Besonderen wurde auf die Anschlüsse für die Informationswissenschaft eingegangen. Es wurde im Text eine Anzahl von Anwendungsbeispielen aufgezählt. Der letzte Teil lieferte eine Diskussion der Möglichkeiten und Probleme mit den Forschungen auf diesem Gebiet.